Multiple Baseline Design: The concept, application, and analysis  

We frequently employ interrupted time series as an evaluation approach to create counterfactuals for impact evaluation. Multiple baseline design is a subtype of interrupted time series design in which the independent variable, i.e., intervention, is altered at several time points for time series (Barlow & Hersen, 1984).  

Multiple baseline designs are based on systematically replicating phase change effects across multiple series, with each following series serving as a control condition for the prior interrupted series.  

Let’s begin with fundamentals. The independent variable, i.e., intervention, is used to investigate the effects of intervention across three categories of dependent variables: behaviors, individuals, and surroundings. In the initial phase, one must collect baseline information on all these dependent variables.  

Once each variable’s baseline is sufficiently stable, the intervention is implemented for one variable while baseline data collection continues for the others. The intervention for the second variable is then carried out if the intervention data for the first variable indicates a trend in the desired direction. This experimental sequence is repeated until all dependent variables stated in the behavior modification program have received the intervention.  

The outcome is measured in each group before any intervention occurs. Further, after sufficient time has passed for it to bring desirable change in the outcome in the first group(s), the outcome is measured in all groups. In the next stage, the intervention is introduced in one or more groups: this process is repeated until all groups receive the intervention. It is important to point out that one can use this design in case of a staggered intervention rollout.  

Multiple baseline design vs stepped wedge design  

Multiple baseline design is different from stepped wedge design. In the case of stepped wedge design, each subsequent rollout is done using a randomized design. In the case of multiple designs, the randomized rollout is not the precondition for employing the design.  

Example 

To explore the idea further, consider an example of impact evaluation using multiple baseline design in the education sector. The situation involves an intervention across several student groups to increase learning outcomes. In this case, repeated baseline measures are collected simultaneously across independent student groups to represent performance before the intervention. Following this, each student group is gradually introduced to interventions. In other words, after collecting acceptable baseline measurements for one student group, the intervention is implemented while the other group(s) are maintained at their baselines. This procedure is repeated until all target populations have been exposed to the intervention.  

The multiple baseline design methodology permits comparisons not just of the dependent variable within baselines but also between baselines. Consequently, while one group receives the treatment, the others serve as controls. 

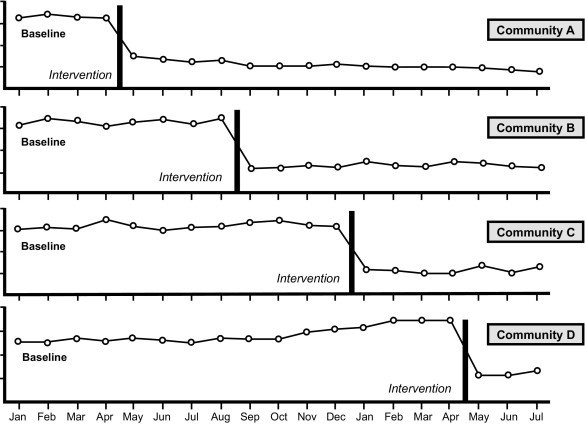
Types of multiple baseline designs classification 

Multiple baseline designs are categorized broadly into three types. 

1.  Multiple baselines across behaviors which investigates two or more of a student’s behaviors 

2. Multiple baseline cross-individual analysis of a particular behavior shared by two or more pupils  

3. Multiple baselines across contexts in which the behavior of a single student is examined in two or more separate situations 

Types of Analysis of Multiple Baseline Design 

One can employ several analytical paradigms for the analysis of multiple baseline designs. 

Visual Analysis 

Visual Analysis is the primary and fundamental tool for analyzing the multiple baseline design. The analytic technique looks for a significant movement in the mean outcome and can be examined visually for such a shift. In visual analysis, we can plot data on a graph where the y-axis represents the dependent variable, and the x-axis represents time units (Zhan & Ottenbacher, 2001). By visually examining the change in slope, we can determine the consistency or reliability of intervention effects (Long & Hollin, 1995). 

Box-Jenkins Method (ARIMA) 

Multiple baseline data are often autocorrelated which means that the value of a measure at any one time may contain a portion of a value measured at an earlier period, which may result in misleading estimates of the intervention effect. Therefore, tools of the ARIMA model (Box-Jenkins technique) can be used to eliminate autocorrelation. It entails transforming time-series data by identifying a model of the dependencies between data points and then employing this model to alter the data to eliminate the dependencies. 

Split-Middle Technique 

Utilizing a split middle methodology with a binomial test is a nonparametric method for analyzing various baseline designs. Using this method, one can look at the nature of the trend in the data by displaying linear trend lines that best suit the data. Further, one can then apply a binomial test to determine if the number of data points in the intervention phase goes above or below the projected line of the baseline (Kazdin, 1982; Kinugasa et al., 2004). 

Multilevel modeling 

We can also use a multilevel model to analyze multiple-baseline design studies, specifically in the case of nested data. In the case of continuous data, such as the mean difference in the outcome, a generalized linear mixed model (GLMM) can be used to estimate both fixed and random effects. One can apply the generalized estimating equation (GEE) methodology for outcomes such as the pass rate. In contrast to GLMMs, which directly model variance and covariance emerging from correlated data, the GEE technique primarily describes population-averaged effects while indirectly accounting for correlation. 

References  

BARLOW, D. H., & HERSEN, M. (1984). Single case experimental designs: Strategies for studying behavior change (2nd ed.). New York: Pergamon. 

KAZDIN, A. E. (1982). Single-case research designs: Methods for clinical and applied settings. New York: Oxford University Press. 

KINUGASA, T., CERIN, E., & HOOPER, S. (2004). Single-subject research designs and data analyses for assessing elite athletes’ conditioning. Sports Medicine, 34, 1035–1050. 

Long, C. G., & Hollin, C. R. (1995). Single case design: A critique of methodology and Analysis of recent trends. Clinical Psychology & Psychotherapy, 2(3), 177-191. 

Zhan, S., & Ottenbacher, K. J. (2001). Single subject research designs for disability research. Disability and rehabilitation, 23(1), 1-8. 

Kultar Singh – Chief Executive Officer, Sambodhi