Difference in Difference: A Brief Overview

History
Difference-in-Difference is one of the most popular quasi-experimental techniques, backed by a large body of historical evidence. Snow (1854) employed the method to determine whether cholera was caused by polluted air or drinking water.
Rose (1952) used DID to study the impact of mediation on labor issues, and Obenauer and von der Nienburg (1915) employed DID to study the effect of the minimum wage. DID is also utilized extensively to assess the impact of immigration on the local labor or to perform labor assessment of supply (Card, 1990).
The Concept
This method compares the differences between treatment and comparison groups, i.e., the first difference, and between the treatment and the comparison group, which is the second difference.
As a quasi-experimental or experiment-based design, this technique uses both baseline and follow-up data from the same treatment group and the control group. For impact evaluations, it is recommended that the DID estimator be used to measure intervention and other treatment impacts.
Assumptions
For DID causality estimation, the following assumptions must be met: positivity, exchangeability, and Stable Value Treatment Assumption (SUTVA).
- Intervention not linked to the outcome at the baseline, i.e., the intervention allocation did not have to be affected by the outcome.
- Treatment/intervention and control groups exhibit parallel outcomes trends.
- Even after multiple cross-sectional designs, the mix of intervention and comparison groups remains steady, with no spillover.
Violation of the Parallel Trends Assumption
The key assumption in the case of DID is the parallel trend assumption, i.e., both groups will have the same patterns across time. The primary assumption is violated when factors can be correlated with treatment status and the timing of treatment.
Also, there may be other things besides treatment that trigger changes in one group but not the other. Various issues that may affect the outcomes include autocorrelation and Ashenfelter dips (in which treatment is assigned based on pre-existing differences).
Analytical Protocol and Estimation
To assess the DID, one may create a dummy variable of treatment and post to conceptualize a regression equation as described below:
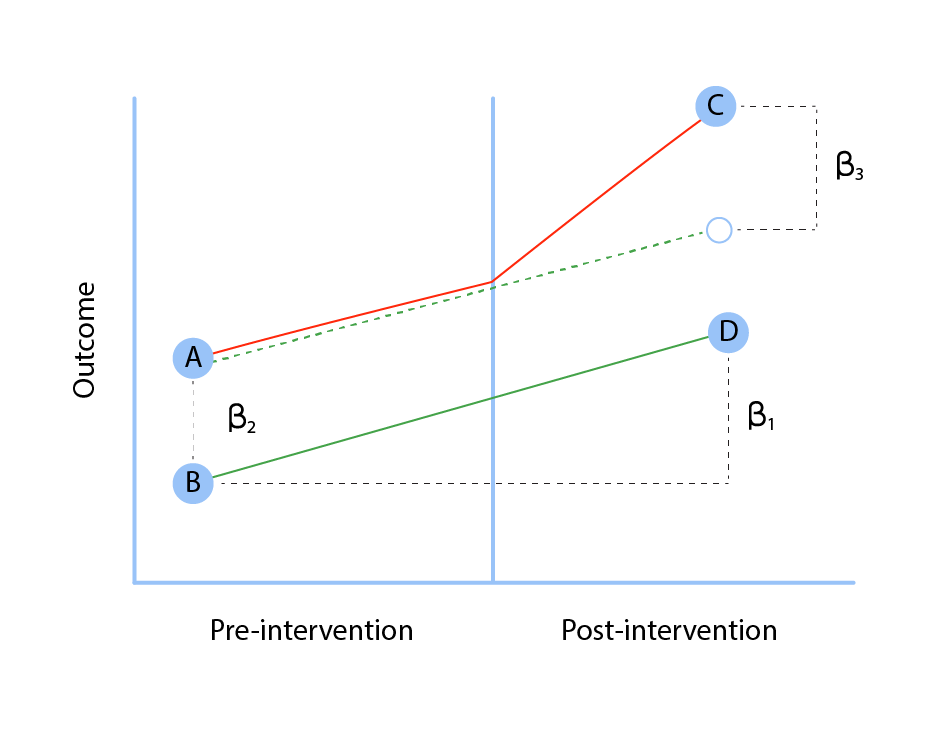
yi = β0 + β1 treatmenti + β2 posti + β3 treatmenti*posti + ei
In the equation, post is a dummy variable that equals 1 for the end line and 0 for before.
When a subject is in a treatment block, the treatment dummy variable is equal to 1; otherwise, it is equal to 0.
The estimate for β3 is the DID estimator. It is the treatment’s differential impact.
β2 depicts the temporal pattern of the control group.
β1 is the difference between the two at the baseline.
Table: DID estimator
| Treatment | Control | Difference | |
| Before | β0 + β1 | β0 | β1 |
| After | β0 + β1 + β2 + β3 | β0 + β2 | β1 + β3 |
| Difference | β2 + β3 | β2 | β3 |
Difference-in-Difference with Covariate
It is crucial to note that in the case of DID, one must control for external variables that may impact the outcome. An appropriate adjustment strategy should adjust for the time-varying variation of covariates between groups, or their impact on time, which can affect the results.
Covariates can be utilized to determine the conditional DiD in various ways like:
· Regression DiD
· Matching
· Weighting approaches, as suggested by Abadie (2005)
Difference-in-Differences with Matching: How it adds value
As the popularity of difference-in-differences has risen, so has the application of matching methods to this study design. The goal of matching is to lessen potential confusion by enhancing the comparability of units within the control and treatment groups.
A subset of possible confounders is selected in the context of difference-in-differences and is compared between units of the treatment and control groups before the intervention. In this way, they attempt to correct for bias due to confounding by balancing variables that are different between the control and treatment groups.
Panel data
It describes the data with multiple observations on the same person, so the data set includes a cross-section and a time-series dimension. The principle concept is to make each unit a self-contained comparator group, comparing its changes over time. Two widely used approaches for obtaining causal estimates are difference-in-difference regression and the fixed-effects model.
A difference-in-difference regression examines two groups of units before and after an intervention, some of which are treated and some of which are not. The difference between treated and untreated units reflects both maturation and treatment effects if there is a change over time.
To calculate the impact of treatment, one subtracts the difference in time between treated and untreated patients.
Multiple Groups and Periods
In reality, DID methodologies can be applied to more than two-time frames. In the DID situation, one could include a complete number of time-dummies into the equation. A general framework analyzed in Bertrand, Duflo, and Mullainathan’s paper (Bertrand, Duflo, and Mullainathan, 2004) and Hansen(2007b) can be valid for many groups and periods. With this framework, one could have a full of temporal effects.
Changes-in-Changes
The concept of changes-in-change (Athey and Imbens 2006) expands DiD to account for different variances in the distribution of outcome variables, not just the average. It allows for estimating ATT or any other changes within the variation in distribution.
Standardized and robust, clustered errors
A major issue with errors in difference-in-difference models is a serial correlation (Bertrand, Duflo, and Mullainathan 2004). The most likely solutions to computing standardized, robust standard errors are:
- Standard errors clustered based on group level
- Clustered Bootstrap, i.e., re-sample of the same group with no single observation
- Averaging into units with two distinct time frames, both post, and pre-intervention.
References
- Abadie, A. (2005), ‘Semiparametric difference-in-difference estimators.’ Review of Economic Studies 72, 1–19
- Abadie, A., & Cattaneo, M. D. (2018). Econometric methods for program evaluation. Annual Review of Economics, 10, 465–503.
- Abadie, A., Athey, S., Imbens, G. W., & Wooldridge, J. (2017). When should you adjust standard errors for clustering?. (No. Working Paper 24003). National Bureau of Economic Research (NBER).
- Ashenfelter, O. (1978). Estimating the effect of training programs on earnings. The Review of Economics and Statistics, 60, 47–57.
- Athey, S., and G. W. Imbens (2006): “Identification and Inference in Nonlinear Difference-In-Difference Models,” Econometrica, 74, 431–497
- Athey, S., & Imbens, G. W. (2017). The state of applied econometrics: Causality and policy evaluation. Journal of Economic Perspectives, 31, 3–32.
- Bertrand, M., Duflo, E., & Mullainathan, S. (2004). How much should we trust differences-in-differences estimates? The Quarterly Journal of Economics, 119, 249–275.
- Blundell, R., & Costa Dias, M. (2000). Evaluation methods for non‐experimental data. Fiscal Studies, 21, 427–468.
- Card, D. (1990). The impact of the Mariel boatlift on the Miami labor market. ILR Review, 43, 245–257.
- Card, D., & Krueger, A. B. (1994). Wages and employment: A case study of the fast-food industry in New Jersey and Pennsylvania. American Economic Review, 84, 772–793.
- Conyon, M. J., Hass, L. H., Peck, S. I., Sadler, G. V., & Zhang, Z. (2019). Do compensation consultants drive up CEO pay? Evidence from UK public firms. British Journal of Management, 30, 10–29.
- Goodman-Bacon, A. (2018). Difference-in-Differences with variation in treatment timing. NBER Working Paper No. 25018. NBER.
- Hansen, C. B. (2007b), ‘Generalized least squares inference in the panel and multilevel models with serial correlation and fixed effects.’ Journal of Econometrics 140, 670–694.
- Lechner, M. (2011). The estimation of causal effects by difference-in-difference methods. Foundations and Trends® in Econometrics, 4, 165–224.
- Obenauer, M. and B. von der Nienburg (1915), ‘Effect of minimumwage determinations in oregon’. Bulletin of the U.S. Bureau of Labor Statistics, 176, Washington, D.C.: U.S. Government Printing Office.
- Rose, A. M. (1952): “Needed Research on the Mediation of Labour Disputes,” Personal Psychology, 5, 187-200.
- Snow J On the Mode of Communication of Cholera. John Churchill; 1855. 216 p
- Wing, C., Simon, K., & Bello-Gomez, R. A. (2018). Designing difference in difference studies: Best practices for public health policy research. Annual Review of Public Health, 39, 453–469.
Kultar Singh – Chief Executive Officer, Sambodhi

