General Linear Models: Definition and Application

General linear models (GLM) go back to the late 18th century, but they were largely brought to life by Carl Friedrich Gauss.   

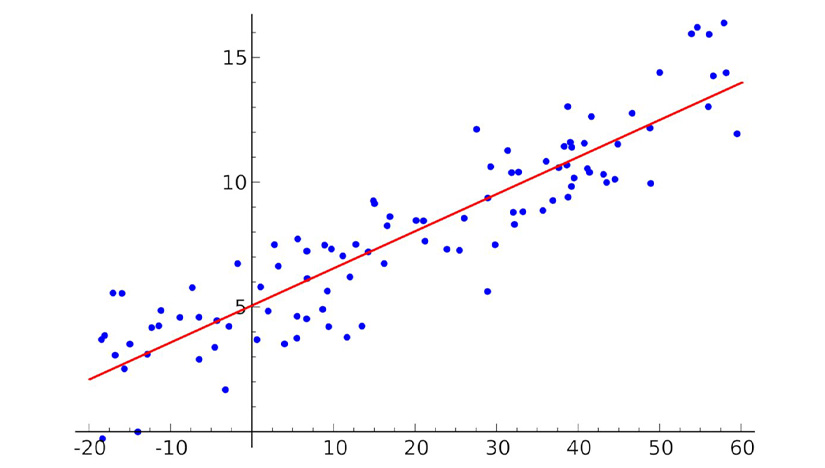
To understand general linear models, we will look at an outcome or response variable indicated by Y and some predictor variable, that is, X. In the linear model, the idea is to create a line representing the data points. It signifies linear regression models for a continuous outcome variable and continuous and/or categorical predictor variable.  

Linear models make three assumptions: 

• The Y’s we observe are not dependent on one another, which means that if we have one value, it doesn’t reveal anything about the next value.
• Every observation is a normal distribution, with a mean μ_i and a variance σ².
• The mean is correlated to the variables that predict outcomes through the linear model.  

GLM is the cornerstone for several statistical tests, including ANOVA, ANCOVA, and regression analysis. In terms of specification, the model data can be described as Data = Model + Error (Rutherford, 2001). The general formula for the general linear model is: 

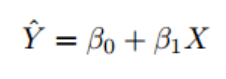
where, Y is the dependent variable, and β₀ is the intercept or constant. β₁ is the coefficient or slope determining the variable’s contribution to the model, and X is the independent variable.  

It is important to note that the critical word in the general linear model is general, and it can handle various variables, including categorical variables. Further, in specific cases where β_s are standardized, they are known as beta weights. 

In its simplest form, a general linear model is one where the model for the dependent variable is a linear combination of independent variables multiplied by a weight that designates the proportionate contribution of each independent variable to the model prediction. 

Linear Regression As A Form Of GLM 

GLM, as described, analyzes the relationship between two variables to determine whether it is statistically significant. Linear regression is the simplest form of the GLM model, wherein it can be used to forecast the value of the dependent variable. The linear regression model can be written with a single independent variable, as in the case of the GLM model written above, including the error term.  

y= β₀+β_x+ϵ 

ANOVA 

ANOVA is a statistical test that compares the means of two or more categorical groups using variance to determine whether there is a statistically significant difference between them. There are various ANOVA test types, and “One-Way” and “Two-Way” are the most popular. The distinction between these two categories is determined by the number of independent variables in a test. 

Generalized Models And Their Difference With General Linear Model 

Generalized linear models are regression models. They model the response variable Y and the random error term based on the exponential family of distributions such as normal, Poisson, Gamma, Binomial, Inverse Gaussian, etc. It presupposes that the response variable’s distribution belongs to the exponential family of distributions. This differs from conventional linear models, i.e., linear regression or ANOVA, in which the response variable, Y, and the random error term, must be based entirely on the normal distribution. 

References  

Cameron A. C. and Trivedi P. K., Regression Analysis of Count Data, Second Edition, Econometric Society Monograph No. 53, Cambridge University Press, Cambridge, May 2013. 

McCullagh, P. and Nelder, J. A. (1989). Generalized Linear Models, Monographs on Statistics and Applied Probability, Vol. 37 of, 2 Edition, Chapman and Hall, London 

Rutherford (2001). Introducing Anova and Ancova: A GLM Approach. SAGE. 

Singh, Kultar. Quantitative Social Research Methods. Los Angeles, CA: Sage, 2007. 
Stroup, W. (2016). Generalized Linear Mixed Models: Modern Concepts, Methods and Applications. CRC Press. 

Kultar Singh – Chief Executive Officer, Sambodhi